백준 17779: 게리맨더링 2

게리맨더링 2 성공

 

 

시간 제한메모리 제한제출정답맞힌 사람정답 비율

1 초

512 MB

8655

5045

3096

56.496%

문제

재현시의 시장 구재현은 지난 몇 년간 게리맨더링을 통해서 자신의 당에게 유리하게 선거구를 획정했다. 견제할 권력이 없어진 구재현은 권력을 매우 부당하게 행사했고, 심지어는 시의 이름도 재현시로 변경했다. 이번 선거에서는 최대한 공평하게 선거구를 획정하려고 한다.

재현시는 크기가 N×N인 격자로 나타낼 수 있다. 격자의 각 칸은 구역을 의미하고, r행 c열에 있는 구역은 (r, c)로 나타낼 수 있다. 구역을 다섯 개의 선거구로 나눠야 하고, 각 구역은 다섯 선거구 중 하나에 포함되어야 한다. 선거구는 구역을 적어도 하나 포함해야 하고, 한 선거구에 포함되어 있는 구역은 모두 연결되어 있어야 한다. 구역 A에서 인접한 구역을 통해서 구역 B로 갈 수 있을 때, 두 구역은 연결되어 있다고 한다. 중간에 통하는 인접한 구역은 0개 이상이어야 하고, 모두 같은 선거구에 포함된 구역이어야 한다.

선거구를 나누는 방법은 다음과 같다.

1. 기준점 (x, y)와 경계의 길이 d1, d2를 정한다. (d1, d2 ≥ 1, 1 ≤ x < x+d1+d2 ≤ N, 1 ≤ y-d1 < y < y+d2 ≤ N)
2. 다음 칸은 경계선이다.
   1. (x, y), (x+1, y-1), ..., (x+d1, y-d1)
   2. (x, y), (x+1, y+1), ..., (x+d2, y+d2)
   3. (x+d1, y-d1), (x+d1+1, y-d1+1), ... (x+d1+d2, y-d1+d2)
   4. (x+d2, y+d2), (x+d2+1, y+d2-1), ..., (x+d2+d1, y+d2-d1)
3. 경계선과 경계선의 안에 포함되어있는 곳은 5번 선거구이다.
4. 5번 선거구에 포함되지 않은 구역 (r, c)의 선거구 번호는 다음 기준을 따른다.
   • 1번 선거구: 1 ≤ r < x+d1, 1 ≤ c ≤ y
   • 2번 선거구: 1 ≤ r ≤ x+d2, y < c ≤ N
   • 3번 선거구: x+d1 ≤ r ≤ N, 1 ≤ c < y-d1+d2
   • 4번 선거구: x+d2 < r ≤ N, y-d1+d2 ≤ c ≤ N

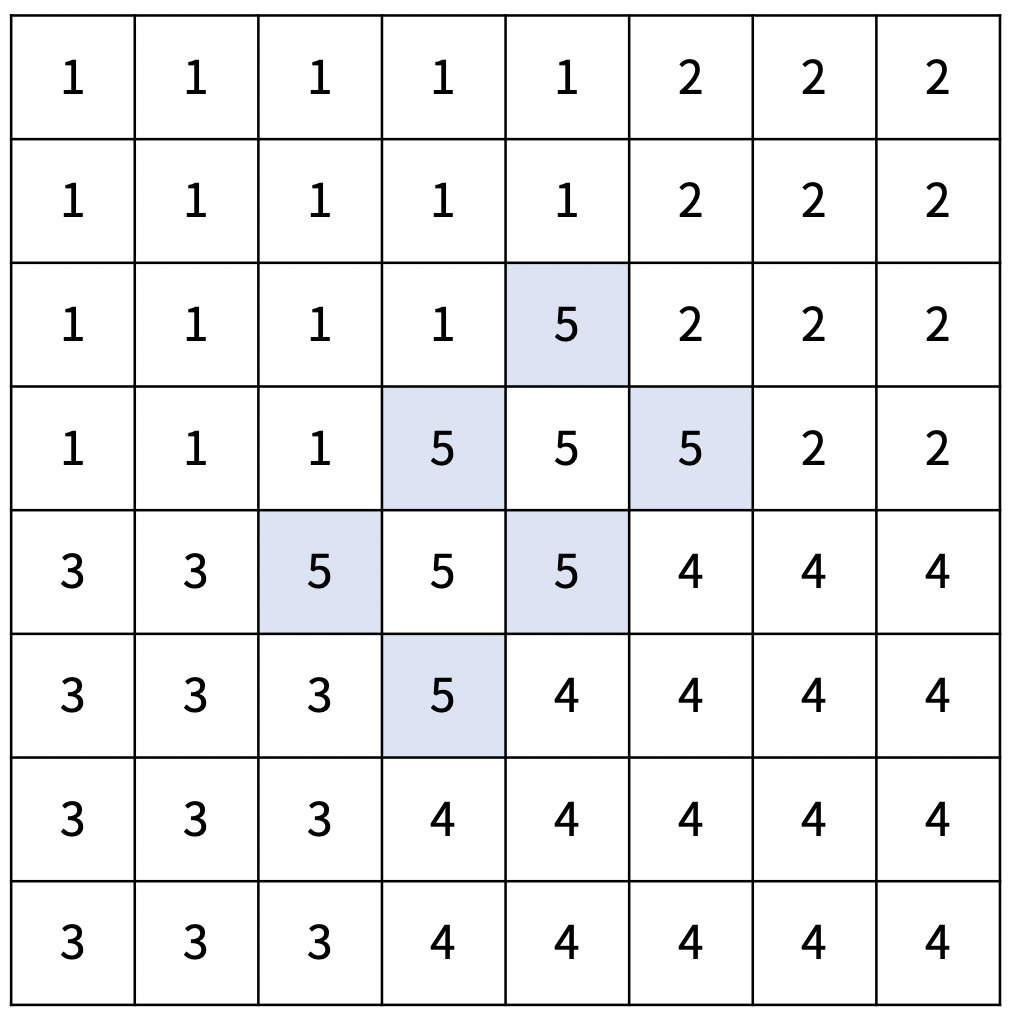
아래는 크기가 7×7인 재현시를 다섯 개의 선거구로 나눈 방법의 예시이다.

x = 2, y = 4, d1 = 2, d2 = 2	x = 2, y = 5, d1 = 3, d2 = 2	x = 4, y = 3, d1 = 1, d2 = 1

구역 (r, c)의 인구는 A[r][c]이고, 선거구의 인구는 선거구에 포함된 구역의 인구를 모두 합한 값이다. 선거구를 나누는 방법 중에서, 인구가 가장 많은 선거구와 가장 적은 선거구의 인구 차이의 최솟값을 구해보자.

입력

첫째 줄에 재현시의 크기 N이 주어진다.

둘째 줄부터 N개의 줄에 N개의 정수가 주어진다. r행 c열의 정수는 A[r][c]를 의미한다.

출력

첫째 줄에 인구가 가장 많은 선거구와 가장 적은 선거구의 인구 차이의 최솟값을 출력한다.

제한

• 5 ≤ N ≤ 20
• 1 ≤ A[r][c] ≤ 100

예제 입력 1 복사

6
1 2 3 4 1 6
7 8 9 1 4 2
2 3 4 1 1 3
6 6 6 6 9 4
9 1 9 1 9 5
1 1 1 1 9 9

예제 출력 1 복사

18

예제 입력 2 복사

6
5 5 5 5 5 5
5 5 5 5 5 5
5 5 5 5 5 5
5 5 5 5 5 5
5 5 5 5 5 5
5 5 5 5 5 5

예제 출력 2 복사

20

예제 입력 3 복사

8
1 2 3 4 5 6 7 8
2 3 4 5 6 7 8 9
3 4 5 6 7 8 9 1
4 5 6 7 8 9 1 2
5 6 7 8 9 1 2 3
6 7 8 9 1 2 3 4
7 8 9 1 2 3 4 5
8 9 1 2 3 4 5 6

예제 출력 3 복사

23

출처

• 문제를 만든 사람: baekjoon

주의! 문제의 x,y가 x축y축이 아니다. 반대로 되어있다.

이것때문에 시간 꽤날려먹었다.

문제 풀이

 

사고과정
기준점 (x, y)와 경계의 길이 d1, d2를 정한다. (d1, d2 ≥ 1, 1 ≤ x < x+d1+d2 ≤ N, 1 ≤ y-d1 < y < y+d2 ≤ N) 
??
훔
다음 칸은 경계선이다.
(x, y), (x+1, y-1), ..., (x+d1, y-d1)
(x, y), (x+1, y+1), ..., (x+d2, y+d2)
(x+d1, y-d1), (x+d1+1, y-d1+1), ... (x+d1+d2, y-d1+d2)
(x+d2, y+d2), (x+d2+1, y+d2-1), ..., (x+d2+d1, y+d2-d1)


x=2,y=4, d1=2, d2 =2
위의 식에 따라 그대로 x,y값을 대입해주면 
(2,4),(3,3),(4,2)
(2,4),(3,5),(4,6)
(4,2),(5,3),(6,4)
(4,6),(5,5),(6,4)
경계선이 이렇게 된다.
1.처음 기준점과 x,y,d1,d2를 
의 기준에 따라서 하나씩 만들고, 
2.각각 만들어진 것들에 따라서 구획을 나눈 뒤 
3.인구수가 가장 큰 구역과 가장 작은 구역이 최소값이 되는 값을 출력하면 된다.

기준
(d1, d2 ≥ 1, 1 ≤ x < x+d1+d2 ≤ N, 1 ≤ y-d1 < y < y+d2 ≤ N) 

1 ≤ y-d1 < y < y+d2 ≤ N 의 조건에 따르면 y는 무조건 2보다 커야한다.
y-d1을 할때 y가 1이라면 d1도 최소1이상이기때문에 0이 되버리니까.
그럼 초기값을
d1=1
d2=1
x=1
y=2
로 해놓고 dfs로 순열을 조건에 맞게 순열을 따라 진행해볼까 한다.

기준을 세분화 해보면
d1,d2>1
1 ≤ x≤ N
x < x+d1+d2 
x+d1+d2 ≤ N
1 ≤ y - d1 < y+d2 
1 ≤ y ≤ N

이렇게 되는데, 코드를 보는게 빠를꺼같다. 걍 구현조건에 맞게 구현하면 된다. 너무 생각을 많이해도 독이되는 문제이다.

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;
int Map[22][22];
int temp[22][22];
int N;
int answer = 987654321;

void build(int x, int y, int d1, int d2) {//구획을 만드는 함수

    if (x + d1 + d2 > N || 1 > y - d1 || y + d2 > N) return;
    int visited[22][22] = { 0 };
    vector<int> v;
    //경계선 그리기
    for (int i = x, j = y; i <= x + d1, j >= y - d1; i++, j--) visited[i][j] = 5;
    for (int i = x, j = y; i <= x + d2, j <= y + d2; i++, j++) visited[i][j] = 5;
    for (int i = x + d1, j = y - d1; i <= x + d1 + d2, j <= y - d1 + d2; i++, j++) visited[i][j] = 5;
    for (int i = x + d2, j = y + d2; i <= x + d2 + d2, j >= y + d2 - d1; i++, j--) visited[i][j] = 5;

    //각 선거구 채우기
    for (int i = 1; i < x + d1; i++) {
        for (int j = 1; j <= y; j++) {
            if (visited[i][j] == 5)break;
            visited[i][j] = 1;
        }
    }
 
    for (int i = 1; i <= x+d2; i++) {
        for (int j = N; j > y; j--) {
            if (visited[i][j] == 5)break;
            visited[i][j] = 2;
        }
    }
    for (int i = x + d1; i <= N; i++) {
        for (int j = 1; j < y - d1 + d2; j++) {
            if (visited[i][j] == 5)break;
            visited[i][j] = 3;
        }
    }
    for (int i = x + d2 + 1; i <= N; i++) {
        for (int j = N; j >= y - d1 + d2; j--) {
            if (visited[i][j] == 5)break;
            visited[i][j] = 4;
        }
    }
    for (int i = 1; i <= N; i++) {
        for (int j = 1; j <= N; j++) {
            if (visited[i][j] == 0)
                visited[i][j] = 5;
        }
    }

    /*for (int i = 1; i <= N; i++) {
        for (int j = 1; j <= N; j++) {
            cout << visited[i][j];
        }cout << endl;
    }*/
    int sum1 = 0, sum2 = 0, sum3 = 0, sum4 = 0, sum5 = 0;
    for (int i = 1; i <= N; i++) {
        for (int j = 1; j <= N; j++) {
            if (visited[i][j] == 1)
                sum1 += Map[i][j];
            else if (visited[i][j] == 2)
                sum2 += Map[i][j];
            else if (visited[i][j] == 3)
                sum3 += Map[i][j];
            else if (visited[i][j] == 4)
                sum4 += Map[i][j];
            else if (visited[i][j] == 5)
                sum5 += Map[i][j];
         
        }
    }
    v.push_back(sum1); v.push_back(sum2); v.push_back(sum3); v.push_back(sum4); v.push_back(sum5);

    sort(v.begin(), v.end());
    int a = v[4] - v[0];
    answer = min(answer,a);
}

int main() {
    cin >> N;
    for (int i = 1; i <= N; i++) {
        for (int j = 1; j <= N; j++) {
            cin >> Map[i][j];
        }
    }
    for (int r = 1; r < N; r++)
        for (int c = 1; c < N; c++)
            for (int d1 = 1; d1 < N; d1++)
                for (int d2 = 1; d2 < N; d2++)
                    build(r, c, d1, d2);
    cout << answer;
    return 0;
}

 

dfs로 완탐을 돌렸는데 그러면 시간초과가 뜬다. 그래서

    for (int r = 1; r < N; r++)
        for (int c = 1; c < N; c++)
            for (int d1 = 1; d1 < N; d1++)
                for (int d2 = 1; d2 < N; d2++)
                    build(r, c, d1, d2);

이렇게 완탐돌려주는게 더 빠르다.